Modelo Preditivo de Óbitos no Trânsito Brasileiro

Modelagem orientada a dados relacionados à segurança viária para o reconhecimento de padrões e previsão de óbitos no trânsito

João Pedro Melani Saraiva

Observatório Nacional de Segurança Viária

Pedro Augusto Borges dos Santos

Observatório Nacional de Segurança Viária

Introdução

Motivação

  • Presente cenário da segurança viária mundial e brasileira (WORLD HEALTH ORGANIZATION, 2023);

  • Diversos países com demanda por modelos estatísticos preditivos (RODRÍGUEZ; JATTIN; SORACIPA, 2020);

  • Defasagem nas fontes de dados: Sistema de Mortalidade - DataSUS;

  • Ocorrência de vítimas fatais no trânsito se relaciona com diversos atributos estruturais, socioeconômicos e ambientais (ZHONG-XIANG et al., 2014);

  • Desenvolvimento do PNATRANS.

Referenciais Teóricos

Objetivo

  • Desenvolver um modelo capaz de prever óbitos em sinistros de trânsito;

  • Explicar a influência e importância das variáveis;

  • Avaliar desempenho de diferentes abordagens (Determinística e Temporal);

  • Avaliar o desempenho de diferentes escalas temporais.

Metodologia

Coleta de dados

  • Dados coletados de diversas fontes, com diferentes escalas de tempo;

  • Diferentes modelos são ajustados de acordo com a disponibiliade de dados:

Variáveis Resolução Temporal
Anual Trimestral Mensal
PIB ✓ ✓ ✓
População ✓ ✗ ✗
Sinistros em rodovias federais ✓ ✓ ✓
Condutores Habilitados ✓ ✗ ✗
Frota veicular ✓ ✓ ✓
Óbitos em sinistros de trânsito ✓ ✓ ✓
  • PIB: BANCO CENTRAL DO BRASIL (2023);
  • População: MINISTÉRIO DA SAÚDE (2023a);
  • Sinistros em rodovias federais: POLÍCIA RODOVIÁRIA FEDERAL (2023);
  • Condutores habilitados: MINISTÉRIO DOS TRANSPORTES (2023a);
  • Frota veicular: MINISTÉRIO DOS TRANSPORTES (2023b);
  • Óbitos em sinistros de trânsito: MINISTÉRIO DA SAÚDE (2023b), coletado utilizando pacote microdatasus (SALDANHA, 2023) da linguagem de programação estatística R.

Modelos

  • Indisponibilidade de dados é um grande obstáculo na confecção de modelos mais complexos e custosos;

  • Diferentes abordagens são testadas a fim de encontrar a metodologia ideal para modelagem da fatalidade dos sinistros.

Modelos Resolução Temporal
Anual Trimestral Mensal
Determinístico
Regressão Linear ✓ ✓ ✓
Random Forest ✗ ✗ ✓
Série Temporal
SARIMA ✗ ✗ ✓
Suavização Exponencial ✗ ✗ ✓

Análise de Série Temporal x Análise Determinística

  • Duas abordagens estatísticas utilizadas no estudo.

  • Análise de Série Temporal:

    • Conjunto de dados em uma sequência cronológica;
    • Sazonalidade e tendência;
    • Autocorrelação e autorregressão;
    • Média móvel.

  • Análise Determinística:

    • Algoritmos de Regressão;
    • Multivariados;
    • Independem da sequência cronológica dos eventos.

Resultados e Discussão

Análise Exploratória de Dados

  • Efetuada para todas as variáveis contempladas;
  • Dados históricos de óbitos no trânsito (variável preditada):

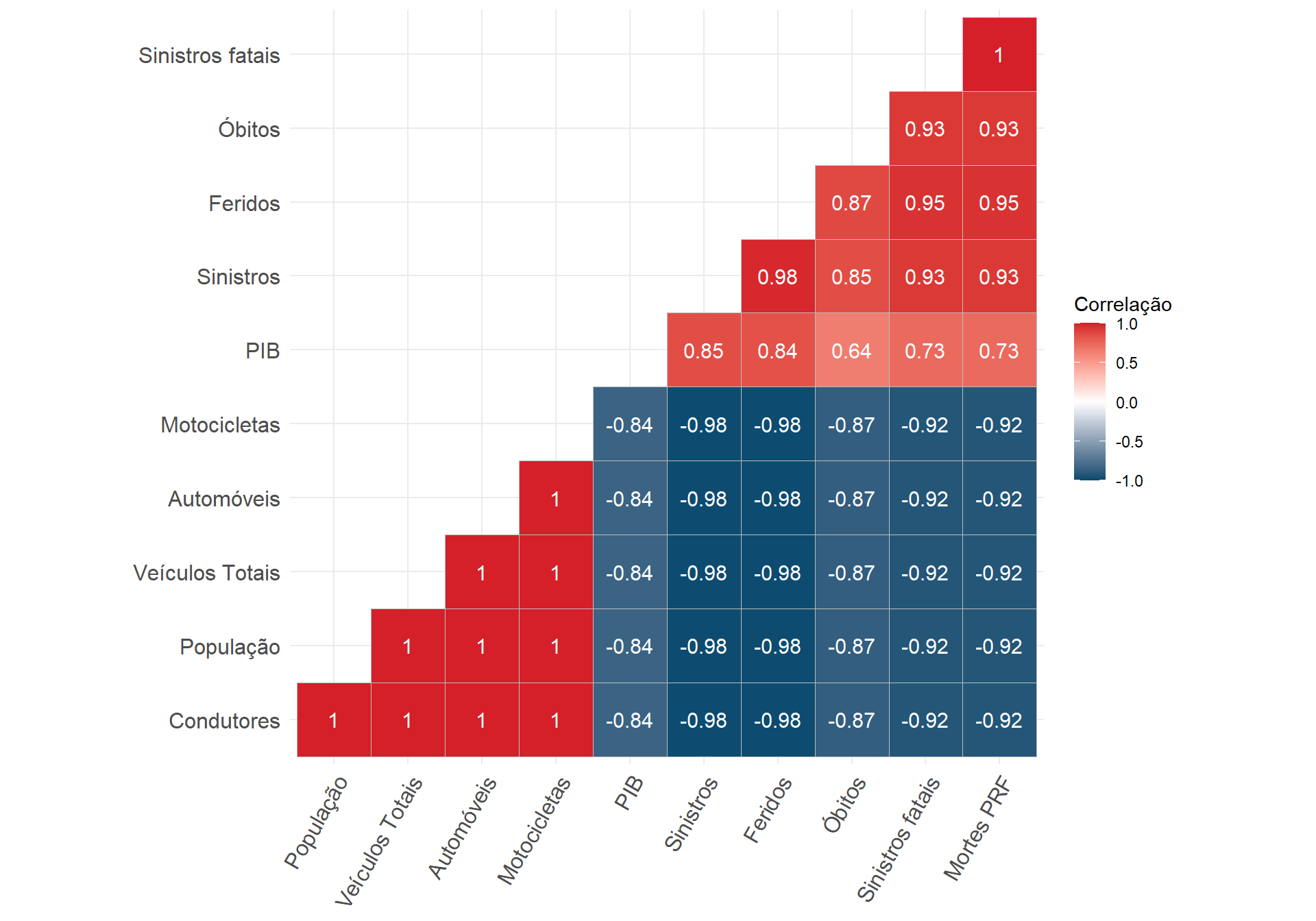
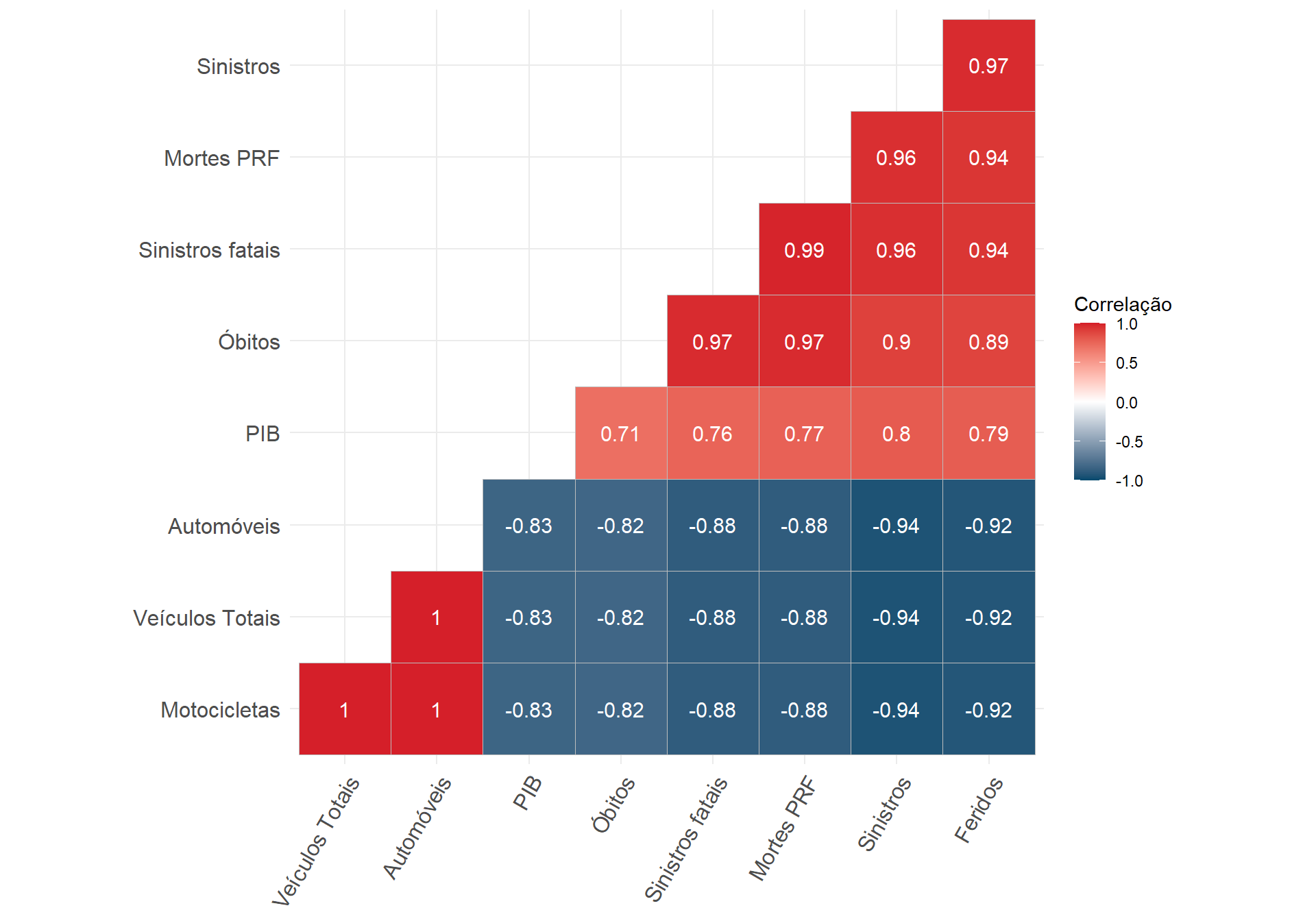
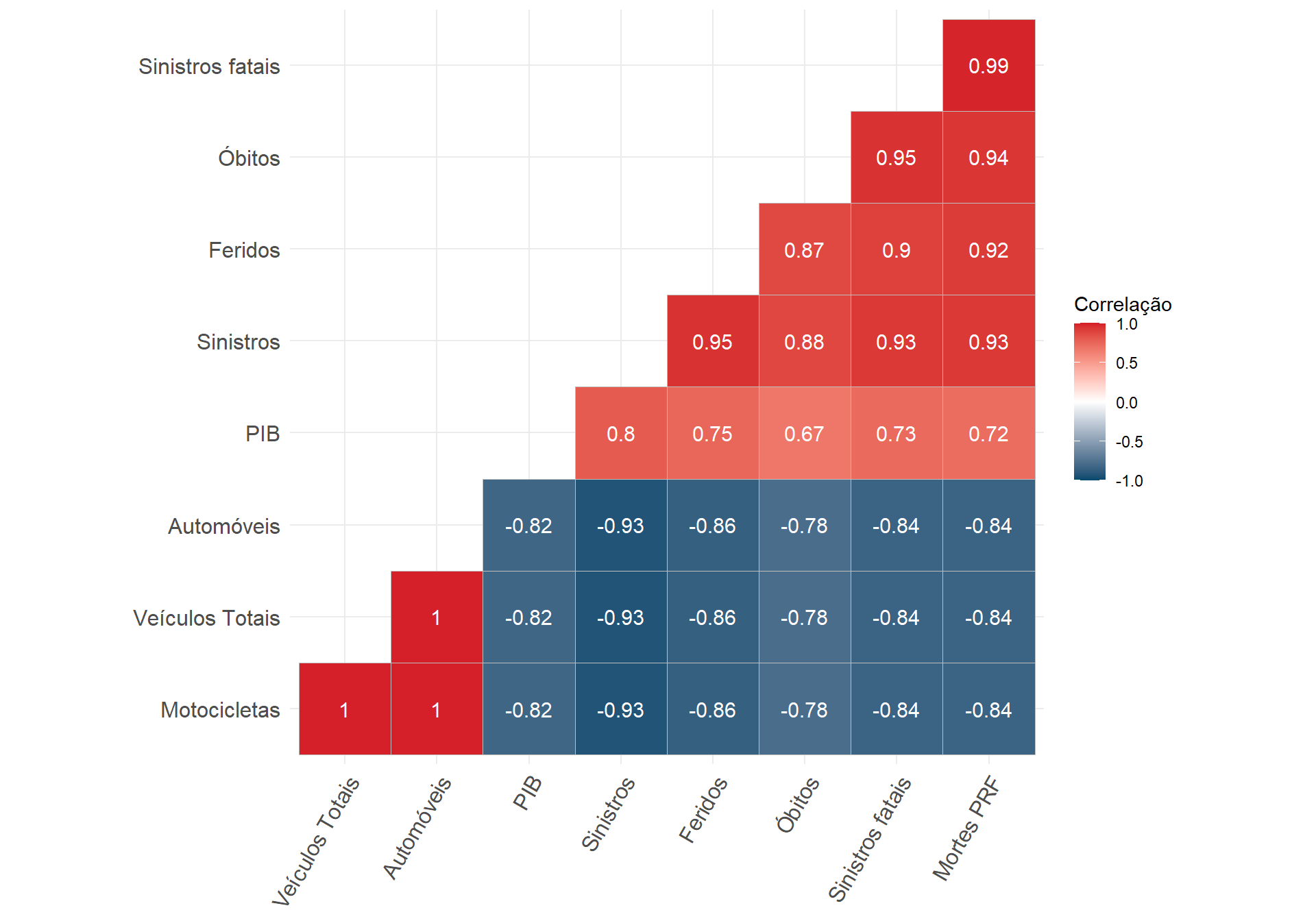
Correlação

  • Correlação não-paramétrica de Spearman (oposta à Pearson);
  • Variação da correlação em relação à resolução temporal;
  • Colinearidade entre diversas variáveis.

Decomposição temporal

Resultados dos Modelos - Regressão Linear

  • Intervalos de confiança amplos;
  • Ajuste sensível à outliers.
Variável Coeficientes p-valor
Intercepto Y 37542.33 0.00
Frota 7214.08 0.35
Sinistros fatais 8525.89 0.03
Sinistros -3804.87 0.30
Condutores -7205.39 0.37

Resultados dos Modelos - Random Forest

  • Reamostragem reduz a colinearidade e sensibilidade à outliers;
  • Algoritmo não produz intervalos de confiança.

Resultados dos Modelos - SARIMA

  • Alta sazonalidade;
  • Amplo intervalo de confiança.

Resultados dos Modelos - Exponential Smoothing

  • Ajuste mais ruidoso;
  • Problemas similares ao SARIMA.

Comparação entre Modelos - Métricas de Erros

Métricas utilizadas:

  • RMSE (Root Mean Squared Error);
  • MAE (Mean Absolute Error);
  • R2 (coeficiente de determinação).
Modelos Métricas
RMSE MAE RSQ
Anual
Regressão Linear 707,61 668,47 0,98
Trimestral
Regressão Linear 314,27 274,95 0,94
Mensal
Regressão Linear 131,02 101,78 0,91
Random Forest Regressor 151,75 105,14 0,92
Exponential Smoothing 154,28 120,24 0,87
SARIMA 139,48 106,69 0,89

Comparação entre Modelos - Previsões de 2023

Modelo Previsão Máx. Mín.
Linear Anual 34.631 37.516 31.747
Linear Trimestral 36.626 38.574 34.677
Linear Mensal 36.950 38.820 35.081
* RF Mensal 34.767 - -
SARIMA Mensal 32.643 35.803 29.484
ETS Mensal 32.812 36.127 29.498
* Algoritmo não produz intervalo de confiança

Custos dos Óbitos

  • O custo financeiro dos 34.631 óbitos previstos pelo modelo anual linear para 2023 foi estimado com base nos custos médios elaborados pelo Instituto de Pesquisa Econômica Aplicada (IPEA) em CARVALHO (2020);

  • O cálculo é corrigido monetariamente utilizando o Índice Nacional de Preços ao Consumidor Amplo (IPCA) acumulado de Dez/2014 à Dez/2023 (fator de 68,14%), por meio de: \[ \begin{aligned} Custo_{\small2023} &= Óbitos_{\small2023} \times Custo_{\small2014} \times (1 + \mbox{IPCA}) \\ &= 34.631 \times \text{R\$ } 433.286,69 \times (1 + 0,6814) \\ &= \text{R\$ } 25.229.661.499,04 \end{aligned} \]

  • Têm-se um custo por óbito de R$ 728.528,24 e um custo total em 2023 de R$ 25.229.661.499,04, ou seja, aproximadamente R$ 25.2 Bi.

Conclusão

  1. Modelos determinísticos aparentam ser mais adequados para previsão;
  2. Óbitos em sinistros são dificilmente modelados utilizando métodos de análise temporal;
  3. Muitas variáveis consideradas são extremamente colineares;
  4. Modelos determinísticos prevêem aumento nos óbitos em 2023;
  5. Possíveis avanços:
    1. Outros métodos de regressão (Ridge, Support Vector, MLP, RNN);
    2. Utilizar indicadores em lugar de variáveis brutas;
    3. Redução da colinearidade (reduzir preditoras, PCA).

Referências

AL-GHAMDI, A. S. Time Series Forecasts for Traffic Accidents, Injuries, and Fatalities in Saudi Arabia. Journal of King Saud University - Engineering Sciences, v. 7, n. 2, p. 199–217, 1995.
BANCO CENTRAL DO BRASIL. SGS - Sistema Gerenciador de Séries Temporais - v2.1. 8 dez. 2023.
BLUMENBERG, C. et al. Is Brazil going to achieve the road traffic deaths target? An analysis about the sustainable development goals. Injury Prevention, v. 24, n. 4, p. 250–255, ago. 2018.
CAI, H.; ZHU, D.; YAN, L. 2015 International Conference on Transportation Information and Safety (ICTIS). Wuhan, China: IEEE, jun. 2015. Disponível em: <http://ieeexplore.ieee.org/document/7232140/>
CARVALHO, C. H. R. Custos Do Acidentes de Trânsito No Brasil: Estimativa Simplificada Com Base Na Atualização Das Pesquisas Do IPEA Sobre Custos de Acidentes Nos Aglomerados Urbanos e Rodovias. [s.l.] Instituto de Pesquisa Econômica Aplicada, 2020. Disponível em: <https://www.ipea.gov.br/portal/images/stories/PDFs/TDs/td_2565.pdf>.
JAFARI, S. A. et al. Prediction of road traffic death rate using neural networks optimised by genetic algorithm. International Journal of Injury Control and Safety Promotion, v. 22, n. 2, p. 153–157, 3 abr. 2015.
JIN, X.; ZHENG, J.; GENG, X. Prediction of Road Traffic Accidents Based on Grey System Theory and Grey Markov Model. International Journal of Safety and Security Engineering, v. 10, n. 2, p. 263–268, 30 abr. 2020.
MINISTÉRIO DA SAÚDE. Mortalidade desde 1996 pela CID-10. 25 set. b2023.
MINISTÉRIO DA SAÚDE. População residente. 25 set. a2023.
MINISTÉRIO DOS TRANSPORTES. Frota de Veículos - 2022. 25 set. b2023.
MINISTÉRIO DOS TRANSPORTES. Registro Nacional de Condutores Habilitados. 25 set. a2023.
POLÍCIA RODOVIÁRIA FEDERAL. Dados Abertos da PRF. 23 set. 2023.
RODRÍGUEZ, J.; JATTIN, J.; SORACIPA, Y. Probabilistic temporal prediction of the deaths caused by traffic in Colombia. Mortality caused by traffic prediction. Accident Analysis & Prevention, v. 135, p. 105332, fev. 2020.
SALDANHA, R. Microdatasus: pacote para download e pré-processamento de microdados do Departamento de Informática do SUS (DATASUS). [s.l: s.n.].
SENETA, E. Markov and the Birth of Chain Dependence Theory. International Statistical Review / Revue Internationale de Statistique, v. 64, n. 3, p. 255, dez. 1996.
WORLD HEALTH ORGANIZATION. Global status report on road safety 2023. [s.l: s.n.].
ZHONG-XIANG, F. et al. Combined Prediction Model of Death Toll for Road Traffic Accidents Based on Independent and Dependent Variables. Computational Intelligence and Neuroscience, v. 2014, p. 1–7, 2014.